Graph Pattern Matching in GSQL
- Blog >
- Graph Pattern Matching in GSQL
In this short technical blog, I will show you how to use GSQL to search a graph for all the occurrences of a small graph pattern. We call this pattern matching.
Consider the problem of matching a pattern of vertices and directed edges in a graph for a single type of vertex. For example, we want to match a given pattern (fig.1) in a graph (fig.2). There are different ways to do the pattern matching, but the basic idea is to pick a reference vertex or edge in the pattern that is a good traversal starting point, and then traverse the graph and try to match the rest of the pattern. I will show you how to do that with two sample solutions.
In the first solution we will start from vertex “A”, and in the second solution, we will start from the edge “B -> C” and use parallel traversal to have 2 symmetrical starting points. For each solution, we have two versions of the query: pattern counting and pattern enumeration. Pattern counting queries only print the occurrence count of the pattern, while pattern enumeration queries list of the specific vertices and edges in each match.
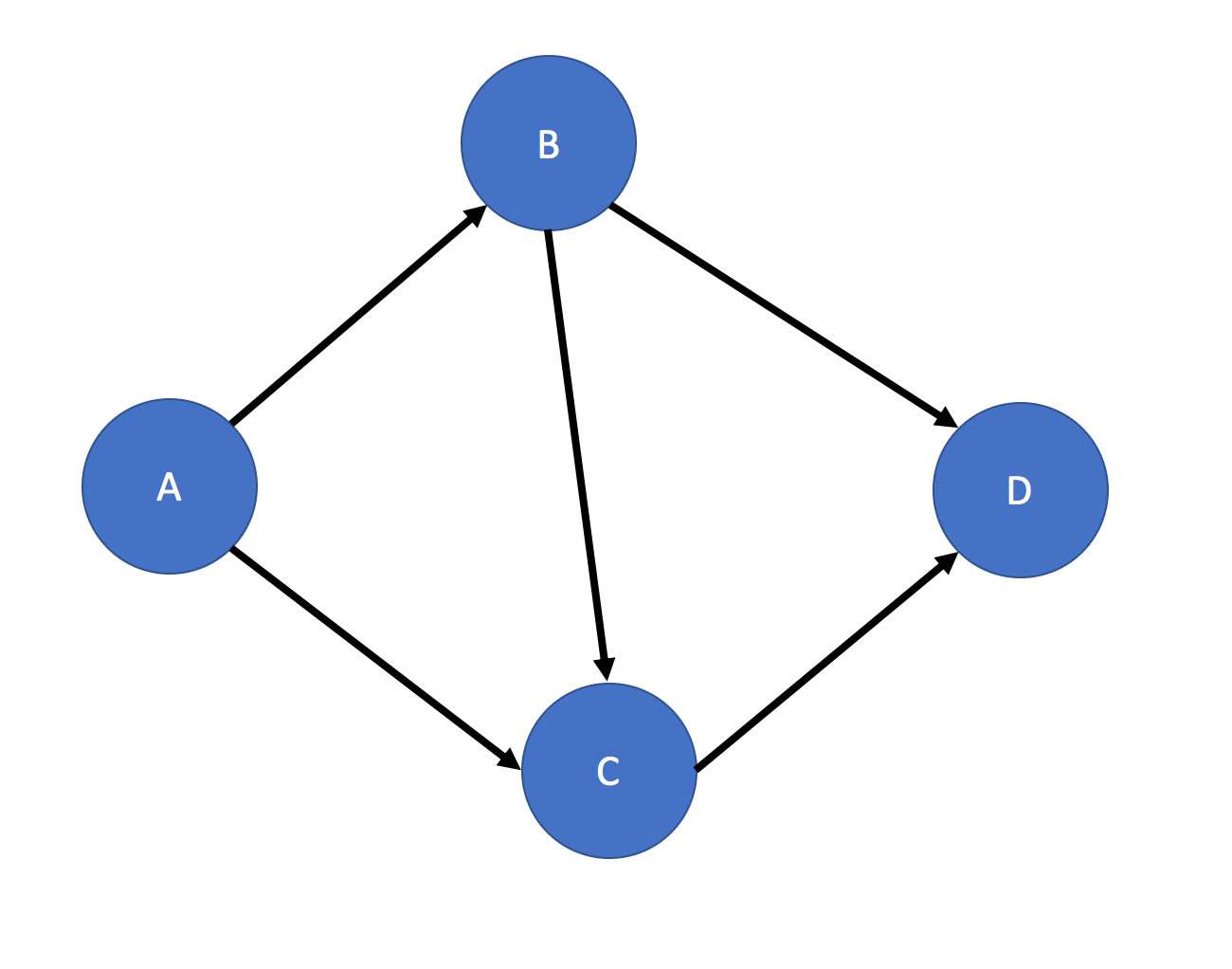
Fig .1 Given Pattern for Pattern Matching
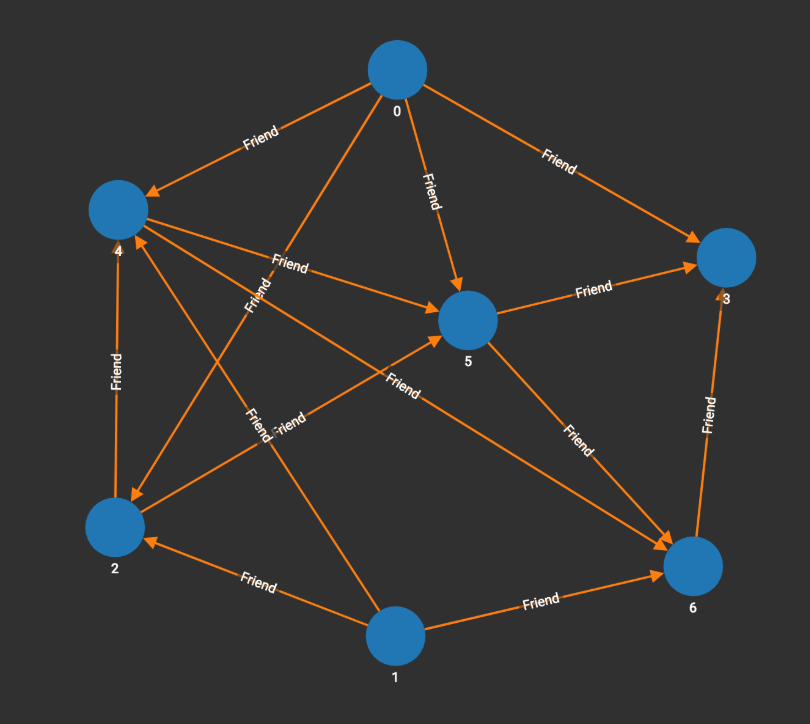
Fig.2 Sample Graph of Social Network
Starting From Vertex “A”
The first solution is to start from each vertex in the graph, treat it as vertex “A” in the pattern, and see if we can successfully traverse in the same pattern as our target pattern. In other words, we can write a subquery whose traversal flow matches our pattern, and which accepts a starting vertex as an input parameter. This vertex will be regarded as vertex “A” in the process of pattern matching. When doing the pattern matching, we can try to find the “B” and “C” vertices first, then an edge from “B” to “C”, and then check whether they have any common 1-hop neighbor (vertex “D”). We can either count the pattern matches, or also show the details of each pattern matched.
Sample Query of Count Patterns:
# sub query: return the number of matched patterns for the source vertex
CREATE QUERY pattern_count_sub(VERTEX source) FOR GRAPH social returns (INT){
OrAccum @is_1hop;
BagAccum<Vertex> @@d;
A = {source};
Hop1 = SELECT b
FROM A:a -(Friend:e) -> Person:b
ACCUM b.@is_1hop = true; // flag for 1-hop neighbors
Hop2 = SELECT c
FROM Hop1:b -(Friend:e) -> Person:c
// check if b and c both have @is_1hop=true -> valid b,c pair
WHERE c.@is_1hop == true
// Count how many neighbors b&c have in common -> d's
ACCUM @@d += b.neighbors("Friend") INTERSECT
c.neighbors("Friend");
RETURN @@d.size();
}
# main query: print the number of matched patterns for each vertex
CREATE QUERY pattern_count() FOR GRAPH social {
MapAccum<Vertex, INT> @@pattern_count;
Start = {Person.*};
Start = SELECT s
FROM Start:s
ACCUM @@pattern_count += (s -> pattern_count_sub(s));
PRINT @@pattern_count;
}
JSON Result:
[
{
"@@pattern_count": {
"0": 2,
"1": 1,
"2": 1,
"3": 0,
"4": 1,
"5": 0,
"6": 0
}
}
]If we also want to print each match of the given pattern, we can add a local nested accumulator to store the patterns, and write the details into a file.
Sample Query for Pattern Enumeration:
# sub query: prints the matched patterns for the source vertex to file
CREATE QUERY pattern_detail_sub(VERTEX source, FILE f) FOR GRAPH social returns (INT){
OrAccum @is_1hop;
MapAccum<VERTEX, BagAccum<VERTEX>> @patterns;
SumAccum<INT> @@cnt = 0;
A = {source};
Hop1 = SELECT b
FROM A:a -(Friend:e) -> Person:b
ACCUM b.@is_1hop = true; // flag for 1-hop neighbours
Hop2 = SELECT c
FROM Hop1:b -(Friend:e) -> Person:c
// check if b and c both have @is_1hop=true -> valid b,c pair
WHERE c.@is_1hop == true
ACCUM b.@patterns += (c -> b.neighbors("Friend") INTERSECT
c.neighbors("Friend"))
POST-ACCUM FOREACH (typeC, typeD) IN b.@patterns DO
IF typeD.size() > 0 THEN
f.println(source, b, typeC, typeD),
//(a, b, c, [d]) [d] is a collection of vertex d
@@cnt += typeD.size()
END
END;
RETURN @@cnt;
}
# main query: call sub query for each vertex
CREATE QUERY pattern_detail(FILE f) FOR GRAPH social {
SumAccum<INT> @@pattern_count;
Start = {Person.*};
f.println("a", "b", "c", "[d]");
Start = SELECT s
FROM Start:s
ACCUM @@pattern_count += pattern_detail_sub(s, f);
PRINT @@pattern_count;
}JSON Result:
[
{
"@@pattern_count": 5
}
]File Output:
a,b,c,[d]
2,4,5,6
4,5,6,3
0,2,4,5
0,4,5,6
1,2,4,5Starting From Edge “B->C”
Another solution is to use the B->C edge as the head of the pattern. Every edge in the graph is a candidate B->C edge, and then we find whether the source and target vertices have common neighbors (“D” and “A”) through both edges and reverse edges. This solution can only be used when the graph contains reverse edges.
Sample Query to Count Patterns:
CREATE QUERY pattern_count_edge() FOR GRAPH social {
SumAccum<INT> @@n_pattern;
Start = {Person.*};
Start = SELECT b
FROM Start:b -(Friend:e) -> Person:c
ACCUM INT through_edge = COUNT(b.neighbors("Friend") INTERSECT
c.neighbors("Friend")),
INT through_rev_edge = COUNT(b.neighbors("Also_Friend") INTERSECT
c.neighbors("Also_Friend")),
@@n_pattern += through_edge * through_rev_edge;
PRINT @@n_pattern;
}JSON Result:
[
{
"@@n_pattern": 5
}
]Sample Query for Pattern Enumeration:
CREATE QUERY pattern_detail_edge(FILE f) FOR GRAPH social {
SumAccum<INT> @@n_pattern;
GroupByAccum<VERTEX typeC, BagAccum<VERTEX> typeA, BagAccum<VERTEX> typeD> @patterns;
Start = {Person.*};
f.println("a", "b", "c", "[d]");
Start = SELECT b
FROM Start:b -(Friend:e) -> Person:c
ACCUM b.@patterns += (c -> b.neighbors("Also_Friend") INTERSECT
c.neighbors("Also_Friend"),
b.neighbors("Friend") INTERSECT
c.neighbors("Friend"))
POST-ACCUM FOREACH (typeC, typeA, typeD) IN b.@patterns DO
IF typeA.size() > 0 AND typeD.size() > 0 THEN
@@n_pattern += typeA.size() * typeD.size(),
FOREACH a IN typeA DO
f.println(a, b, typeC, typeD)
END
END
END;
PRINT @@n_pattern;
}JSON Result:
[
{
"@@n_pattern": 5
}
]File Output:
a,b,c,[d]
1,2,4,5
0,2,4,5
0,4,5,6
2,4,5,6
4,5,6,3To try these queries in the sample graph, please click on the Github link below and follow the instructions: https://github.com/Suxiaocai/blog_examples/tree/master/pattern_match