The Beauty of Graph Algorithms with Built-in Parallelism
- Blog >
- The Beauty of Graph Algorithms with Built-in Parallelism
Many people already know that graph algorithms are the most efficient and sometimes the only solution for complex business use cases, such as clustering different groups of users (Community Detection), finding influential persons or entities (PageRank Algorithm), or predicting user behaviors for personalized recommendation (Label Propagation Algorithm). However, it is not commonly known that Graph is also the ideal approach to solve problems where there might be an unknown number of joins to connect two entities. This type of problem is common across verticals including use cases such as enterprise knowledge, supply chain analytics, and energy flow computation.
This blog describes how Graph can solve these problems in a natural, concise, and efficient way and can provide answers in subseconds, even when traversing hundreds of millions of entities and relationships.
Problem Description
Let us consider a simple example in analyzing relationships between companies.
There is only one table Ownership ( company, owner, percentage) with three columns where each row describes the percentage of a company owned by an owner.
Business Query (Output): find the top K “final owner” companies which own the most of Company A. A final owner is a company which is not owned by any other company.
Inputs: name of Company A, integer K
As an example, given Company 1 as the input in Figure 1, Company 9 owns the most of Company 1.
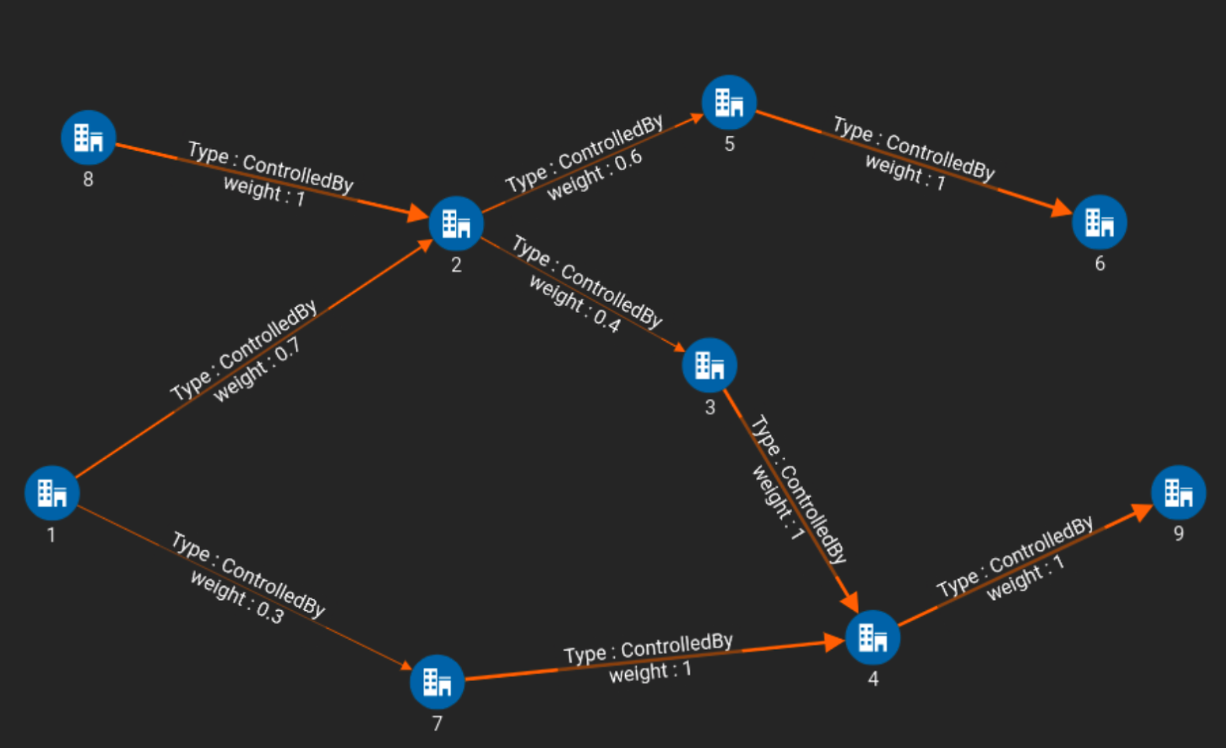
Figure 1
Challenges
There are two challenges:
1. Unknown number of joins. We don’t know how many levels/steps away a company X may have ownership of Company A (directly or indirectly).
2. There might be multiple paths with different number of steps from Company A to a company X which has ownership in Company A. For example, Company X may have ownership in Company A through 5 intermediate companies on one path while may also have ownership in Company A through 3 intermediate companies on another path. Furthermore, the 5 intermediate companies on one path and the 3 intermediate companies on the second path may or may not overlap.
As an example in Figure 1, Company 9 owns Company 1 via two paths with different lengths. RDBMS and NoSQL DBs aren’t designed to handle multiple hops (joins) efficiently. Moreover, standard SQL does not have any way to express “join repeatedly until you reach a target.” Furthermore, on big datasets, the computational time and effort on non-graph DBs and even on older generation graph DBs is prohibitive. The reason is that those architectures do not have the vertex-centric parallel computation that is needed to do the work minimally and efficiently. They wastefully join entire tables, even though most of the table is not relevant.
The above type of problems occur in many industries and use cases. For example, in supply chain management, we can have a Bill of Materials Table BOM ( Part, Parent_Part, Quantity ). Each row describes that a Part (first column) is one of the components needed to make the Parent_Part (second column), and the third column describes how many Part units are needed to make one Parent_Part. Again we have the same two challenges as described above: A Part X may depend on a Part Y through an unknown number of steps. There are many business questions which need to traverse the Part dependency graph along different paths with different steps. For example,
-Compute whether an order of some final products can be satisfied with the current inventory of all the parts needed.
-Compute the pricing change of final products if the price of some parts change.
-Electric power grids also need to address these challenges. If one or more component goes offline, the utility needs to know what effect this has on downstream and upstream components and power lines.
Graph Solution with Built-in Parallelism
Now we describe how we can use a Graph DB with built-in parallelism in its graph query language, such as TigerGraph and its query language GSQL, to easily and efficiently solve this type of problem. Parallelism is important because it is the natural and efficient way to implement many graph-oriented problems. Computer scientists who’ve studied some graph algorithms know that they often have steps which start with “For each vertex / For each edge / For each neighbor of vertex V…” These “for each” conditions mean that we need to do the same task for each member in a set. If the set is large, the efficient way to do the work is in parallel. GSQL features built-in parallelism, so that it is very easy to express these “for each” tasks.
There are a few approaches to solve this company ownership problem, which illustrates the power and flexibility of GSQL. In TigerGraph’s parallel read-compute-update execution flow, a query or algorithm behaves like a distributed walk or traversal of the graph: We start from a designated set of vertices and then follow a plan for step-by-step walking or traversing to neighboring edges. Along the way, we gather data from vertices or edges. We can pass along data to the vertices we encounter, or save it for the end.
Approach 1
The high-level idea is to go through the company ownership graph in two passes. Each pass begins with Company A and propagates through ownership edges. The first pass is essentially a preparation stage. It simply computes for any Company Y the number of companies Company Y directly owns which also have ownership in Company A. This computed number on each such Company Y is used in the second pass to make sure each company completely sums up all ownership in Company A it has before it propagates its ownership of Company A to the companies which directly own it. For example, in Figure 1, Company 4 stores the number 2, because two of its in-neighbors have ownership of Company 1.
The second pass propagates percentages of ownership of Company A to all companies directly or indirectly owning Company A. Each owner company waits until it receives an ownership message from the number of direct owners computed in the first pass,. It then takes the total ownership of Company A it has received and propagates fractions of that amount to its owners. For our example of Figure 1, Company 2 waits until it receives 1 message (70% ownership). After receiving this, it sends messages to its owners. It sends the message “42%” (70% x 0.6) to Company 5 and “28%” (70% x 0.4) to Company 3.
Note that we only compute the total ownership of each owner Company Y only one time, which is efficient. In use cases like supply chain and energy flow analysis, the propagative computations they need (e.g., the change in price, voltage, or current) are much more compute-intensive, so efficient single-pass computation across the graph is important to real-time performance.
Please see the GSQL query in Figure 2. The complete solution including graph model and GSQL queries are available at TigerGraph’s github repository.
CREATE QUERY getOwnershipPert (vertex<Company> inputComp) FOR GRAPH MyGraph {
SumAccum<int> @msgCnt1, @msgCnt2;
OrAccum<bool> @visited;
SumAccum<float> @score = 0;
SetAccum<vertex> @@results;
Start = {inputComp};
WHILE Start.size() > 0 limit 8 DO
Start = SELECT t FROM Start:s-(ControlledBy:e)-:t
ACCUM t.@msgCnt1 += 1
POST-ACCUM s.@visited = true
HAVING t.@visited == false; // don't start again for the second visit;
end;
Start = {inputComp};
Start = SELECT s FROM Start:s ACCUM s.@score = 1; // initialize @score
WHILE Start.size() > 0 LIMIT 8 DO
Start = SELECT t FROM Start:s-(ControlledBy:e)-:t
ACCUM t.@msgCnt2 += 1, t.@score += s.@score * e.weight
POST-ACCUM
CASE WHEN t.outdegree("ControlledBy") == 0 THEN
@@results += t
END
HAVING t.@msgCnt2 == t.@msgCnt1; // make sure got all the scores
END;
Start = @@results;
Start = SELECT s FROM Start:s ORDER BY s.@score desc LIMIT 5;
PRINT Start;
}Approach 2
The expressiveness of a high-level graph query language with built-in parallelism, such as GSQL, means we can efficiently express business logic which would be very cumbersome in the low-level APIs for NoSQL, and even impossible in SQL. Our second approach does not need the preparation stage of the first approach. The idea is to utilize the business knowledge that the ownership of Company A by Company Y is accumulative. This means we can compute the ownership of company along each path separately, and if multiple paths intersect at a vertex, we can simply add the contribution by each path, regardless of when a path reaches that shared vertex. .
Referring to Figure 1 for an example, in Round 2, Company 7 tells its neighbor Company 4 that it owns 30% of Company. So, in Round 3, Company 4 tells its neighbor Company 9 that it owns 30% of Company A. However, also in Round 3, Company 3 tells Company 4 that it owns 28% of Company A. Therefore in Round 4, Company 4 gives Company 9 an update, telling it that is owns an additional 28% of Company A.
CREATE QUERY getOwnershipPertDelta(vertex<Company> inputComp) FOR GRAPH MyGraph {
SumAccum<float> @deltaOld, @deltaNew, @score;
SetAccum<vertex> @@results;
Start = {inputComp};
Start = SELECT s FROM Start:s ACCUM s.@score = 1, s.@deltaOld = 1;
WHILE Start.size() > 0 LIMIT 8 DO
Start = SELECT t FROM Start:s-(ControlledBy:e)-:t
ACCUM t.@deltaNew += s.@deltaOld * e.weight
POST-ACCUM
t.@score += t.@deltaNew,
t.@deltaOld = t.@deltaNew,
t.@deltaNew = 0,
CASE WHEN t.outdegree("ControlledBy") == 0 THEN
@@results += t
END;
END;
Start = @@results;
Start = SELECT s FROM Start:s ORDER BY s.@score desc LIMIT 5;
PRINT Start;
}Conclusion
Real world problems (such as supply chain optimization, routing logistics, , enterprise knowledge graph, fraud prevention, risk management, and others can be complex, due to the highly interconnected data. RDBMS and non-graph NoSQL DBs are not designed to express and to solve these type of important problems. Developers do not want to hard code a solution in Java or C++ either, which can be time-consuming, error-prone, hard to maintain and reuse, no parallel or distributed capability. A solution using high-level graph query language with built-in parallelism is the only solution and it’s a beautiful solution too.