Implementing a 24-Join SQL Query in a Graph Database
- Blog >
- Implementing a 24-Join SQL Query in a Graph Database
Many people are unaware that some difficult-to-write and inefficient-to-execute SQL queries can be easily expressed and efficiently executed in a graph database. This is true even for some people who already know that graph algorithms are the most efficient and sometimes the only solution for complex business use cases—such as user clustering (using the Louvain modularity algorithm), finding influential persons or entities (using the PageRank algorithm), or predicting user behaviors for personalized recommendation (using label propagation algorithms).
In this article we describe a 24 SQL join query in the enterprise knowledge graph space and shows that it can be equivalently solved in a graph database in a way which is easy to understand, easy to maintain and more efficient in query execution. The example use case comes from a problem described in a community discussion forum: https://community.tigergraph.com/
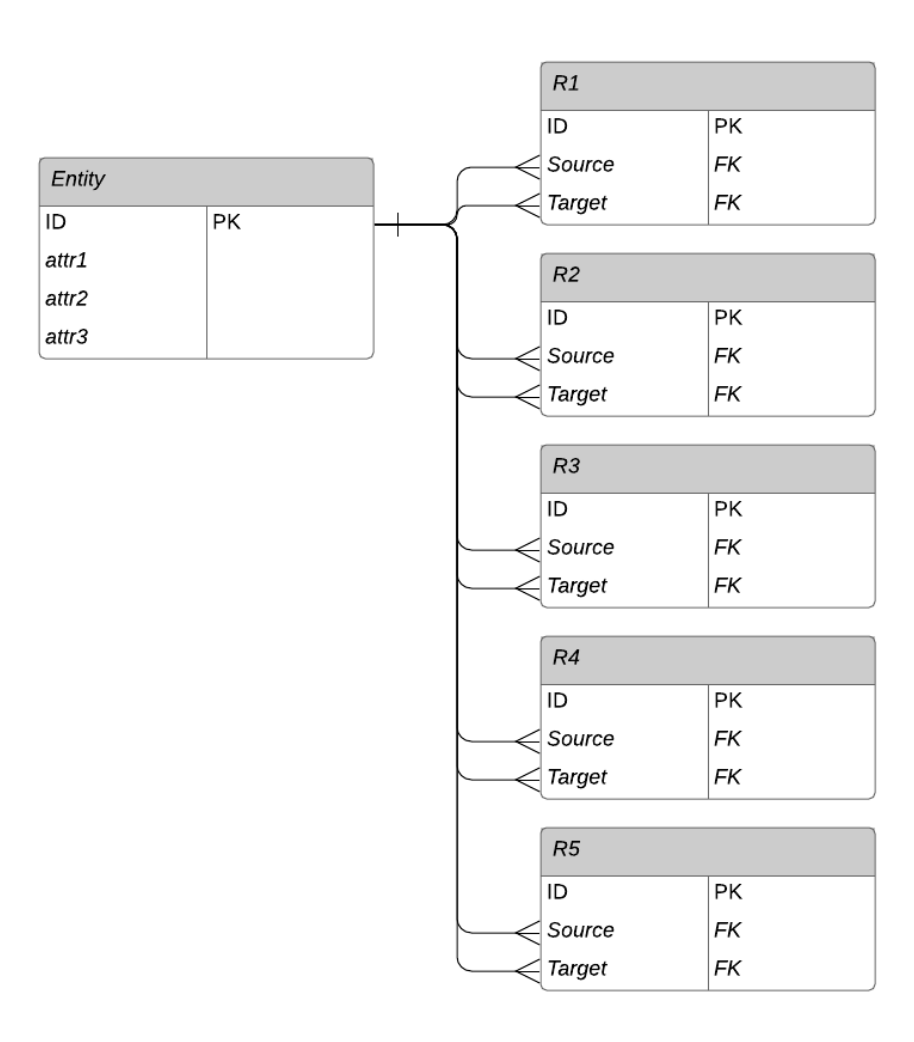
Figure 1. Relational database schema for our example
The high level description of the business question is to find entities which have at least three specified relationships to other entities, and the connected entities in turn also need to have at least 3 other specified relationships. More specifically, the problem is to find each and every distinct entity X such that:
X has an R1 type relationship to an entity A which has
– an R1 type relationship to any entity, AND
– an R2 type relationship to any entity, AND
– an R3 type relationship to any entity
AND X has an R2 type relationship to an entity B which has
– an R2 type relationship to any entity, AND
– an R3 type relationship to any entity, AND
– an R4 type relationship to any entity
AND X has an R3 type relationship to an entity C which has
– an R3 type relationship to any entity, AND
– an R4 type relationship to any entity, AND
– an R5 type relationship to any entity
Each of the 12 conditions links one entity to another. All of the entities are stored in one table, so we are repeatedly referring back to that table. In addition, the full problem has conditions on the attribute values of the entities. If we lay out one particular solution to the query, showing individual entities rather than tables, it could look like Figure 2 below:
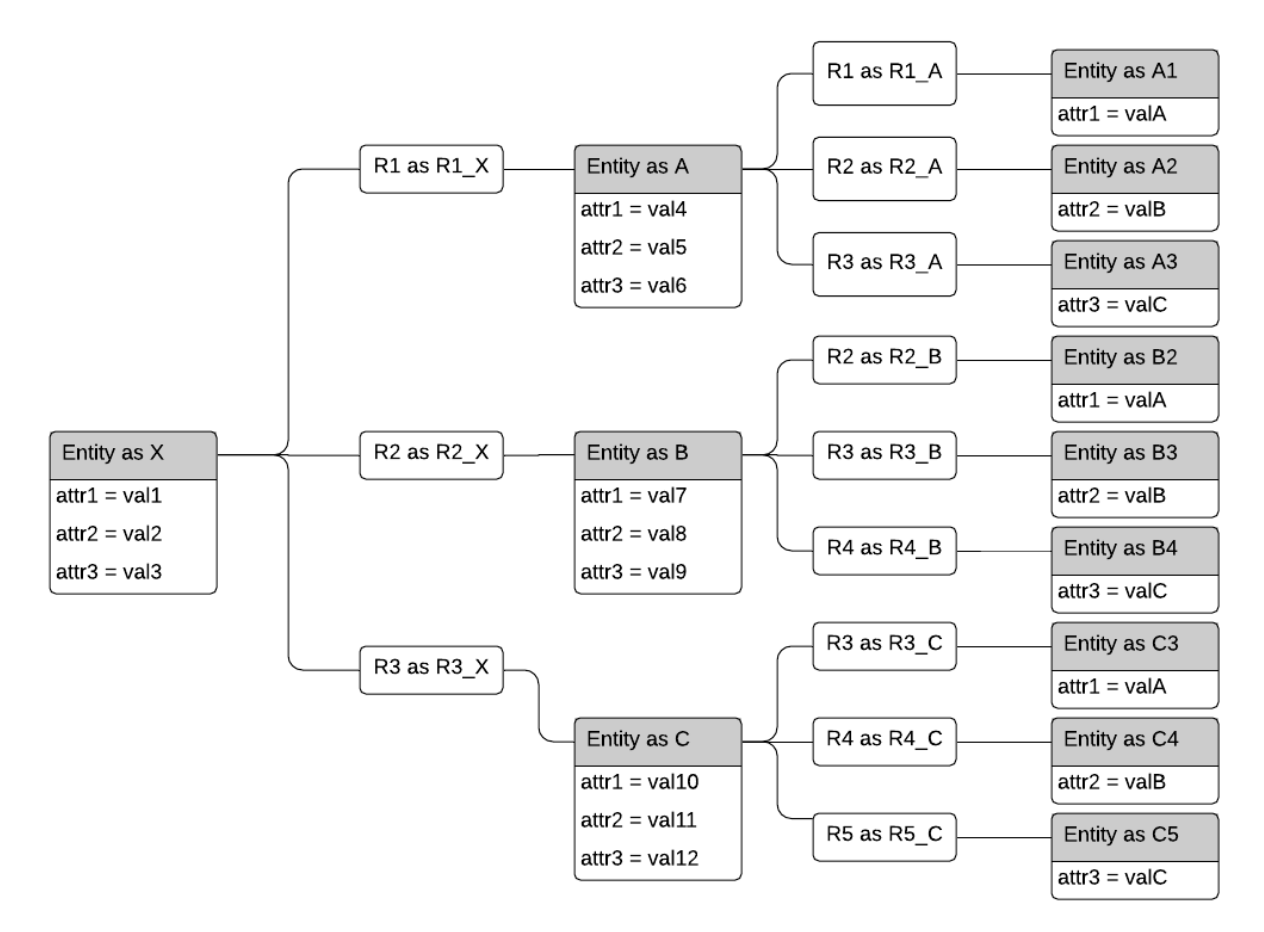
Figure 2. Symbolic representation of a solution to the query
This query is not as artificial as it may seem. Suppose the entities are bank accounts, and the relationships are fund transfers from one account to another. This sort of tree pattern could be an example of layering, a technique used by money launderers to disguise their activity. Or, it could be tracing the trickle-down effect from payments originating from entity X — an employer, a foundation, or a government agency.
This depiction is helpful for designing and understanding how to write this query in SQL, shown below:
SELECT DISTINCT Entity.id
FROM Entity AS X
JOIN R1 AS R1_X ON Entity.id = R1_X.source
JOIN Entity AS A ON A.id = R1_X.target
JOIN R1 AS R1_A ON A.id = R1_A.source
JOIN R2 AS R2_A ON A.id = R2_A.source
JOIN R3 AS R3_A ON A.id = R3_A.source
JOIN Entity AS A1 ON R1_A.target = A1.id
JOIN Entity AS A2 ON R2_A.target = A2.id
JOIN Entity AS A3 ON R3_A.target = A3.id
JOIN R2 AS R2_X ON Entity.id = R2_X.source
JOIN Entity AS B ON B.id = R2_X.target
JOIN R2 AS R2_B ON B.id = R2_B.source
JOIN R3 AS R3_B ON B.id = R3_B.source
JOIN R4 AS R4_B ON B.id = R4_B.source
JOIN Entity AS B2 ON R2_B.target = B2.id
JOIN Entity AS B3 ON R3_B.target = B3.id
JOIN Entity AS B4 ON R4_B.target = B4.id
JOIN R3 AS R3_X ON Entity.id = R3_X.source
JOIN Entity AS C ON C.id = R3_X.target
JOIN R3 AS R3_C ON C.id = R3_C.source
JOIN R4 AS R4_C ON C.id = R4_C.source
JOIN R5 AS R5_C ON C.id = R5_C.source
JOIN Entity AS C3 ON R3_C.target = C3.id
JOIN Entity AS C4 ON R4_C.target = C4.id
JOIN Entity AS C5 ON R5_C.target = C5.id
WHERE
Entity.attr1 = val1 AND
Entity.attr2 = val2 AND
Entity.attr3 = val3 AND
A.attr1 = val4 AND
A.attr2 = val5 AND
A.attr3 = val6 AND
A1.attr1 = valA AND
A2.attr2 = valB AND
A3.attr3 = valC AND
B.attr1 = val7 AND
B.attr2 = val8 AND
B.attr3 = val9 AND
B2.attr1 = valA AND
B3.attr2 = valB AND
B4.attr3 = valC AND
C.attr1 = val10 AND
C.attr2 = val11 AND
C.attr3 = val12 AND
C3.attr1 = valA AND
C4.attr2 = valB AND
C5.attr3 = valC
Notice that, in the above SQL query, there are 12 joins on the relationship tables, 12 more joins back to (copies of) the Entity table, and then a lengthy set of conditions on the attributes of the various entities.
Problems of the SQL Solution
The 24 Join SQL solution is difficult to write, understand and maintain. In fact, we had considerable difficulty knowing which copy of a table was which, until we drew Figure 2 with the alias for each table shown. Moreover, it is well known that relational databases find it very challenging to perform more than a handful of joins in a single query. A query like this is simply not possible unless the tables are very small.
Graph Solution with Built-in Parallelism
Now we describe how we can use a graph database with built-in parallelism in its graph query language, such as TigerGraph and its query language GSQL, to easily and efficiently solve this type of problem.
We first redraw the schema and the solution expansion as a graph. In a graph, each Entity record becomes a vertex, drawn as a circle, and each Relationship record becomes an edge, drawn simply as a line connecting two Entities. Edges can have properties too, such as time or location or strength, but this particular example doesn’t have edge properties. While the schema looks different, the solution expansion is simply a streamlined version of the relational solution expansion.
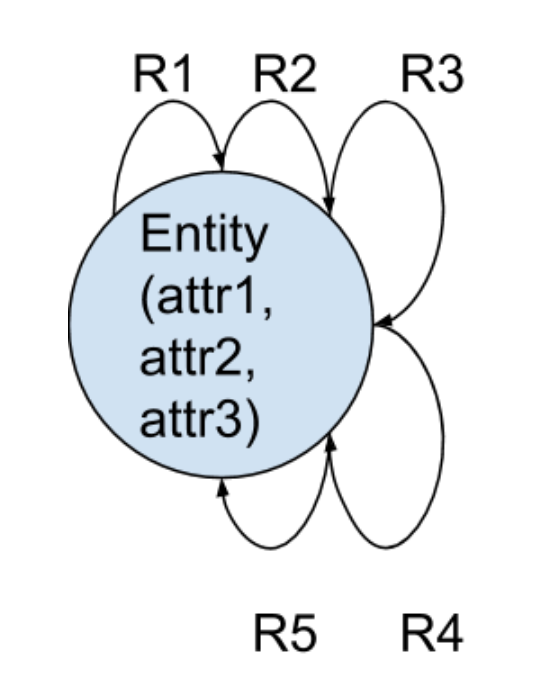
Figure 3. Graph schema for this example
The graph schema diagram may look unusual to you if you are not familiar with graphs. It is saying there is one type of Entity, which has 3 attributes (attr1, attr2, and attr3). In addition, there are five types of relationships — R1 through R5 — each of which connects an Entity to another Entity, with an explicit sense of direction.
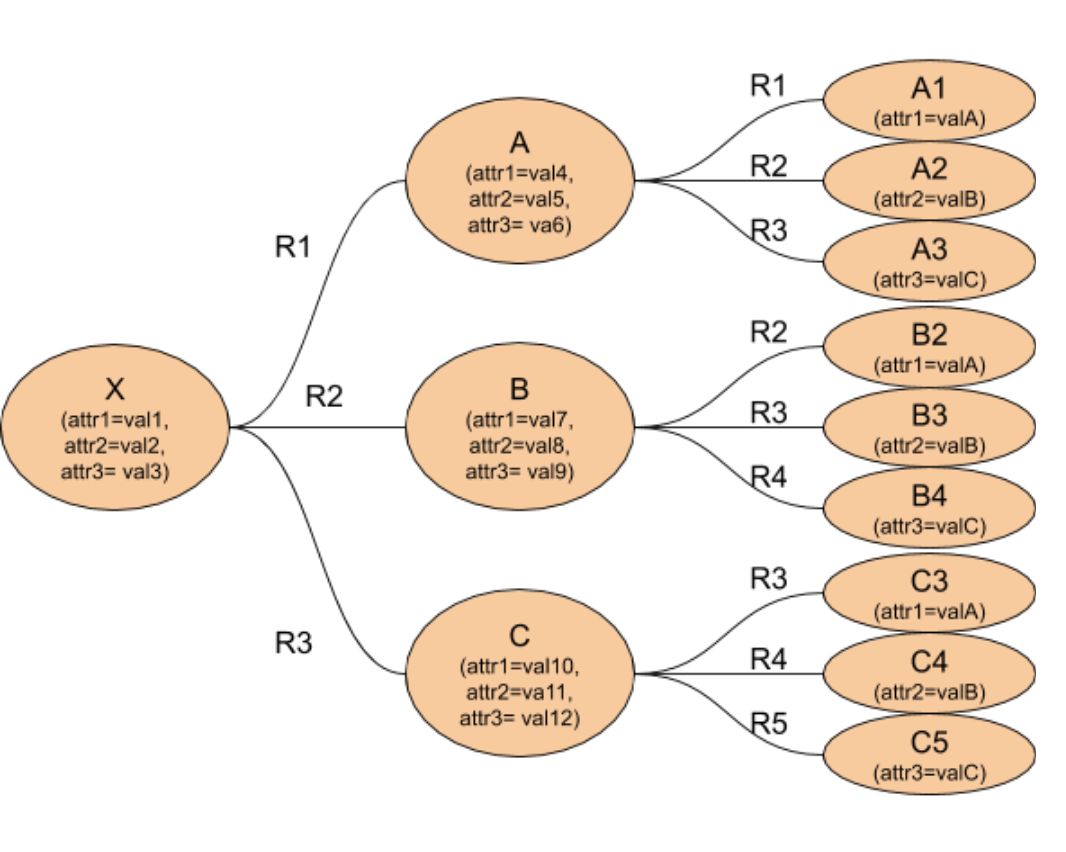
Figure 4. Graph depiction of the query.
There are different approaches to solve this problem due to the power and flexibility of GSQL. The following shows one way of solving the program.
Entities = {Entity.*};
/* Compute qualified A entities based on attribute conditions and downstream relationships */
A =
select m from Entities:m-(R1)-:t
where m.attr1 == val4 and m.attr2 == val5 and m.attr3 == val6
and t.attr1 == valA;
A=select m from A:m-(R2)-:t where t.attr2== valB ;
A=select m from A:m-(R3)-:t where t.attr3 == valC ;
/* Compute qualified B entities based on attribute conditions and downstream relationships*/
B =select m from Entities:m-(R2)-:t
where m.attr1 == val7 and m.attr2 == val8 and m.attr3 == val9 and t.attr1 == valA;
B=select m from B:m-(R3)-:t where t.attr2 == valB
B=select m from B:m-(R4)-:t where t.attr3 == valC;
/* Compute qualified C entities based on attribute conditions and downstream relationships*/
C = select m from Entities:m-(R3)-:t where m.attr1 == val10 and m.attr2 == val11 and m.attr3 == val12 and t.attr1 == valA;
C=select m from C:m-(R4)-:t where t.attr2 == valB;
C=select m from C:m-(R5)-:t where t.attr3 == valC;
/* Compute qualified X entities based on attribute conditions and relationships to A, B, and C */
X1 = select t from A:s-(R1)-t
where t.attr1 == val1 and t.attr2 == val2 and t.attr3 == val3;
X2 = select t from B:s-(R2)-t;
X3 = select t from C:s-(R3)-t;
Result = X1 intersect X2 intersect X3;
print Result;
Graph Solution Advantages
Clearly the graph solution is much easier to write, read, understand and maintain than the huge single 24 join SQL query. The graph solution can also be easily extended to go beyond the current ‘two level’ checking on the join structure without losing performance and readability.
Learn More
One of the best ways to get started with graph analytics is with TigerGraph Cloud. It’s free and you can create an account in a few minutes. Sign up here.
Download these buyer’s guides if you would like to compare the performance of different graph databases: TigerGraph vs Neo4j and TigerGraph vs Amazon Neptune.
You can also learn more about TigerGraph by joining our community: https://community.tigergraph.com/. We look forward to hearing from you.