Improving Route Management with Advanced Analytics Powered by Graph Analytics
- Blog >
- Improving Route Management with Advanced Analytics Powered by Graph Analytics
Why We Need Route Management
Without efficient commodity shipping systems, online shopping can not gain its popularity today. By 2040, long-haul freight shipping by truck in the U.S. may reach 460 million miles per day. Nowadays, freight shipping companies are facing the challenge of fast-growing demands for short lead times and flexible delivery slots. Meanwhile, shipping companies are also under pressure from aggressive competition, making it more difficult to keep the balance between cost-efficient delivery and competitive service levels.
Route management is the practice of improving shipping efficiency. In a manual route planning process, when shipping orders come in, the fleet managers will assign the orders to different routes, and coordinate drivers and trucks for the shipping trips after taking the driver availability, historic traffic condition, weather condition, and other factors into consideration. In general, a good route management strategy tries to maximize the revenue by increasing the number of shipping orders and minimize the cost by reducing shipping mile and elapsed time for each trip. However, with the increasing demand for delivery performance in terms of speed, accuracy, and predictability manual route planning is no longer a viable approach. Using computer algorithms for route management can reduce planning time, provide more accurate estimated time for arrival or ETA, and improve customer experience. In this article, we will describe the data science best practices for applications of graph algorithms in route management.
Graph Problems in Route Management
Many problems in route management are essentially graph problems. For example, searching the shortest path to the destination is one of the most commonly seen problems in route management. The problem can be described in graph by representing each stop as a vertex and using the edge to describe the reachability relationship between the stops. Many graph algorithms are also available for the shortest path problem. In the next part, we will dive into how the route management is related to another classic graph problem: finding the maximal independent sets (MIS).
What is MIS?
In graph theory, an independent set is a set of vertices where none of the vertices in the set are adjacent in the graph. A maximal independent set (MIS) is an independent set that is not a subset of any other independent set. In other words, there is no vertex outside the independent set that may join it because it is maximal with respect to the independent set property.
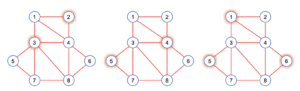
Figure.1. left: vertices 2 and 3 form an independent set in the graph. It is not a maximal independent set, since it is a subset of the independent set {2, 3, 6}. middle: {4, 5} is a maximal independent set. right: {1, 5, 6} is also a maximal independent set of the graph.
Finding MIS is useful in many optimization problems. For example, the freight shipping companies would like to optimize their truck arrangement to help more customers with commodity shipment. To fully utilize the resource, the company wants to assign a truck with as many shipping trips as possible, however, some of the shipping trips can conflict with each other. For example, trip A (SJ – SF in Fig.2) may require arriving at San Francisco at 7 am, and trip B (SJ – LA in Fig.2) may require arriving at Los Angeles at 8 am on the same day. Since Los Angeles is over 5-hour drive from San Francisco, so one truck cannot take both trip A and trip B. Considering the above constraint, such a route management problem can be formed as: given a set of trips, to find the largest subset of trips where the trips in the subset do not conflict. As we describe above, solving this problem is equivalent to finding the maximal independent set in a graph where the trips are represented as vertices, and the “conflict” relationships are represented as edges.
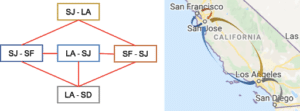
Figure. 2. left: Each vertex in the graph represents a trip (FROM – TO). Each edge connects two trips that cannot be combined. right: Locations of the cities. (SJ: San Jose, SF: San Francisco, LA: Los Angeles, SD: San Diego)
Blelloch’s Algorithm
Blelloch’s algorithm is one of the most straightforward and flexible ones for finding the MISs. The algorithm can be implemented with the following steps.
- Assign each vertex with a unique order (integer) and two labels: selected = False and activated = True (Fig. 3 left).
- Find the activated vertices with the highest order among its neighbors, and set their label to selected = True, activated = False.
- Find the neighbors of previously selected vertices (in step 2) and set their label activated to False. (Fig. 3 middle)
- Repeat step 2 and 3 until no activated vertex in the graph. (Fig. 3 right)
- Return the selected vertices as the MIS.
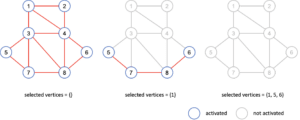
Figure. 3. left: each vertex is initialized with a unique order (smaller number means higher order). middle: vertex 1 has the highest order among its neighbors, and it will be selected and deactivated first. After vertex 1 is selected, all of its neighbors will also be deactivated. right: In the second iteration, among the activated vertices, both vertices 5 and 6 have the highest order within its activated neighbors, so they will be also selected.
As we have shown in Fig. 3, a graph can have multiple MISs of different sizes. Finding the MISs of the largest size is a notorious NP-hard problem, as it requires finding all the MISs, and the number of MISs can grow exponentially with the size of the graph. Using Blelloch’s algorithm, different orderings can be applied to the vertices to generate different MISs, and an approximated largest MIS can be obtained by comparing the size of each MIS.
Graph Database to the Rescue
There is an urgent need for improvement in delivery performance regarding speed, accuracy, predictability, as well as cost and efficiency. The ever-growing size of the shipping trip data and the running time requirement for the route planning query post a great challenge on the data storage and analysis. Graph database offers a solution with its massively parallel processing capabilities. The MIS algorithm described above is a parallel algorithm, meaning the computation on each vertex can be processed independently. For example, in step 2, one thread can handle one edge computation where the order of the target vertex is aggregated to the source vertex. After the source vertices collected all the order from their neighbors, each of the source vertices can determine if they will be selected independently. Such a computation model can naturally fit into a map-reduce framework and can be run efficiently on graph databases.